A Walkthrough on a Weisfeiler-Lehman Isomorphism Test Implementation in Python

Mateus Souza · September 7, 2021

Algorithms   Graph Theory

Weisfeiler-Lehman is an algorithm to test if two graphs (G and H) are isomorphic.

Two graphs are considered to be isomorphic if they contain the same number of vertices and they’re connected in the same way [2].

Well, it may be easy to identify in some cases like in the below image, its pretty obvious that those are isomorphic graphs.

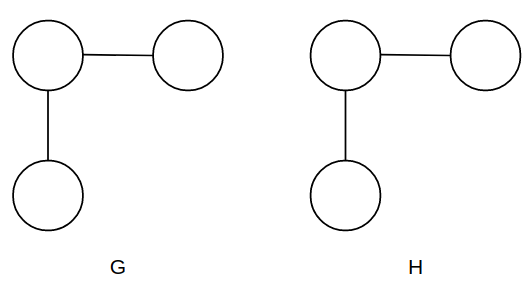
Isomorphic Graphs 1

However sometimes it can be a boring and hard task as the graphs are not similar designed, like this:

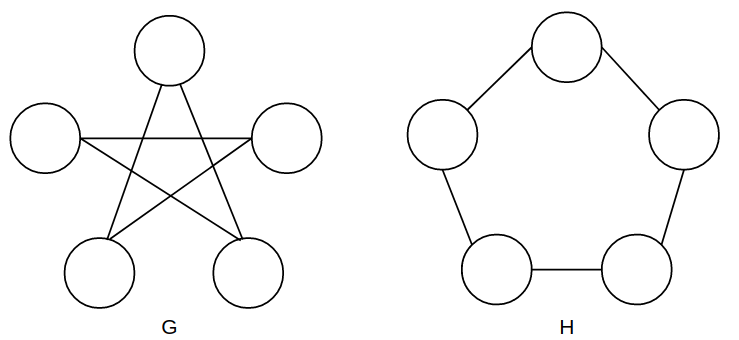
Isomorphic Graphs 2

So that’s why it’s a good idea to have an algo to do the work for us.

*Obs: Weisfeiler Lehman test isnt garenteed to determinate if a graph is isomorphic to other as there are cases the test will fail. it can only say for sure that two graphs are not isomorphic, and they may be isomorphic.

How does that work?

The core idea of the Weisfeiler-Lehman isomorphism test is to find for each node in each graph a signature based on the neighborhood around the node. These signatures can then be used to find the correspondance between nodes in the two graphs, which can be used to check for isomorphism [1].

Walkthrough

This is a walkthrough on my wl algorithm implementation, the full code can be found on my Github.

def run_wl(graph_one: Graph, graph_two: Graph) -> bool:
    """ run wl algo
    
    Args:
        graph_one (Graph): first graph
        graph_two (Graph): second graph
    Returns:
        bool: maybe these graphics are isomorphic
    """
    
		# if the graph hasnt same vertice count, surely they cant be
		# isomorphic
    if graph_one.vcount() != graph_two.vcount():
        return False

		# setting all vertices of both graphs to have label 1
    __set_all_as_one(graph_one)
    __set_all_as_one(graph_two)
        
    graph_one_vs_count = graph_one.vcount()

    for i in range(graph_one_vs_count):

				# iteraing by vertice of each graph
        for j in range(graph_one_vs_count):
            nodeg1 = graph_one.vs[j]
            nodeg2 = graph_two.vs[j]

						# creating a multiset based on their neighbors label
            nodeg1['metadata'] = {
                'multiset': [
                    graph_one.vs[x]['name'] for x in graph_one.neighbors(nodeg1)
                ]
            }
            
            nodeg2['metadata'] = {
                'multiset': [
                    graph_two.vs[x]['name'] for x in graph_two.neighbors(nodeg2)
                ]
            }

				# comparing both graphs multiset partition
        multiset_one, multiset_two = __gather_multisets(graph_one, graph_two)

				# if they have different partition at any interarion, they are not
				# isomorphic
        if normalized_mutual_info_score(multiset_one, multiset_two) != 1.0:
            return False

				# otherwise, we recolor each vertex with their multiset hash
				# and continue the algorithm
        __recolor_vertex(graph_one)
        __recolor_vertex(graph_two)
		
		# if we got here, maybe they're isomorphic
    return True

How can I run it?

I strongly recommend you to run this project using Pipenv + pyenv, as you can activate pipenv shell and easily get dependencies by running:

$ pipenv shell
$(pipenv active) pipenv install
$(pipenv active) python3 main.py
..
...

Important Files

main.py: main file to run algo

service_graph.py: wrapper to graph library

wl_algo: file that contains wl algo

data.graphs.py: file that holds default example graphs

Dependencies

  • jgraph
  • igraph
  • python-igraph
  • cairocffi
  • scikit-learn

References:

[1] The Weisfeiler-Lehman Isomorphism Test, David Bieber available here.

[2] Isomorphic Graphs, Math World, available here.

Twitter, Facebook